En el diagrama estático la carga puntual aplicada da
lugar a solicitaciones de corte y flexión que son de fácil calculo con los
métodos delas ecuaciones fundamentales del equilibrio, permitiendo conocer los
esfuerzos y las deformaciones en la sección longitudinal de la viga. Pero si la
carga P es puesta de forma dinámica la flexión va a variar en un tiempo que
involucra aceleraciones, que por el principio de D’Alambert crean fuerzas
inerciales que se oponen al movimiento.
Estas fuerzas inerciales tiene una magnitud que resulta
de fundamental importancia en los análisis dinámicos en los sistemas
estructurales y no solo dependen de la intensidad de la carga P sino de la masa
y flexibilidad de la estructura. Es de importancia conocer las fuerzas de
inercia previa al aplicar las tensiones.
Las respuestas dinámicas están definidas en un tiempo
determinado pero generadas en las coordenadas que dan libertad de movimiento a
la estructura. Las ecuaciones que permiten saber los distintos desplazamientos
en estos casos se conocen por ecuaciones de movimiento o desplazamiento un
sistema que está compuesto por una masa solida concentrada a nivel del dintel
de un pórtico elemental de un piso como se ve en la figura. Cuando la masa
puede moverse de forma horizontal presentando una traslación simple el
movimiento en la dirección es resistido por la rigidez de la columnas,
comportándose como resortes con una constante k el amortiguamiento del complejo
representando un embolo a la fricción con una constante a amortiguamiento C.
La definición de este amortiguamiento es la absorción de
energía del sistema donde es proporcional a la velocidad de la masa, el factor
de amortiguamiento es una medida de la capacidad de disipación de energía de la
estructura. Un sistema sometido a una fuerza externa todo el conjunto de
fuerzas sobre esa masa está formulada, la ecuación de equilibrio dinámico.
- F1 = Mü son las fuerzas de inercia.
- FD = Cύ son las fuerzas de amortiguamiento.
- FS = Ku son las fuerzas elásticas.
La variable u es el desplazamiento,
ύ es la velocidad, siendo esta la primera derivada de u con respecto al tiempo,
y ü es la aceleración, producida por la
segunda derivada de u con respeto al tiempo. La masa M, C constante de
amortiguamiento y k la constante de resorte.
Sustituyendo tenemos que a ecuación es
igual a.
La carga dinámica que se aplica a la estructura es la
variable P. cuando se produce una eventualidad sismológica, el sistema se
analiza como lo expresa la siguiente figura donde no se aplican fuerzas
externas por lo cual la carga P=0 denotando que la sumatoria sería igual a cero
en la ecuación anterior. En los sismos el desplazamiento proviene del suelo
siendo ug y la aceleración de la base üg,
determinando un desplazamiento total de la masa ut. La diferencia más notable
que hay entre una situación dinámica un evento sísmico, el primero existe una
fuerza exterior, y el segundo el movimiento depende del suelo, por lo tanto el
desplazamiento es relativo de la masa respecto a la base.
Por lo tanto la fuerza de inercia se calcula.
Esto es para el caso para P=0 se expresa así.
Y despejando.
Si se comparan las ecuaciones de la fuerza dinámica con
la de un sismo. Se deduce que en un sismo es equivalente a una carga dinamia
igual al producto de la aceleración del suelo por la masa de la estructura
conocida como carga efectiva sísmica. En la ecuación anterior el termino dela
derecha con signo negativo de la igualdad nos dice que la carga efectiva actúa
en dirección opuesta a la aceleración del suelo. Este producto Müg resulta la carga efectiva producida por el movimiento del
suelo.
La ecuación del producto negativo permite resolver
problemas estructurales solicitados por movimiento sísmicos, pero en el caso de
sistemas de amortiguamiento y no amortiguamiento se debe usa.
W, representa la frecuencia circular de la vibración no
amortiguada, en rad/seg permitiendo la obtención de la frecuencia natural en un
sistema f en un periodo de tiempo T.
La frecuencia cíclica del movimiento se conoce como f
Vibraciones libre sin amortiguamiento
Las respuestas
dinámicas de una estructura es más simple cuando la vibración libre sin
amortiguamiento, P=0 en este caso la ecuación es.
Cuando
se considera una frecuencia circular.
Con
la solución de esta ecuación diferencial.
A y B corresponden a las constantes de amplitud de la respuesta de
la vibración libre y dependen de la velocidad inicial ύ0 y el desplazamiento
inicial u0 del complejo estructural. Expresando estas constantes en términos de
estas condiciones iniciales se obtiene la ecuación del movimiento.
El movimiento armónico simple se indica de forma sinusoidal
según las condiciones iniciales del desplazamiento U0 y la pendiente ύ= para el
tiempo inicial T=0. La amplitud de las vibraciones es.
Vibraciones libre con amortiguamiento
La capacidad de una estructura de
perder energía durante el movimiento es conocido como amortiguamiento, lo cual
incide efectivamente en disminuir la respuesta debida a las acciones sísmicas.
En el movimiento vibratorio es producido un amortiguamiento que va a impedir
que el complejo vibre por siempre, esto el movimiento se retarda con una
variación gradual de vibraciones hasta que termine la oscilación.
Básicamente
se encuentran tres tipos de amortiguamiento.
- Amortiguamiento viscoso.
- Fricción exterior.
- Fricción interna del material elástico.
En
el primero de estos amortiguamientos cuando se desplaza una mase dentro de un
fluido denso, como el caso de los émbolos. Es un sencillo de representar en
forma de ensaya de laboratorio y produce un decrecimiento exponencial de la
vibración. Cuando es por fricción externa producida por el roce contra la
superficie seca el decrecimiento de la vibración es de forma lineal en este
caso.
En el caso de los complejos estructurales es más fácil
percibir un amortiguamiento por fricción interna del material elástico que se
trata de la pérdida paulatina de energía del sistema que está en vibración, al
dispar la energía por fricción dentro de las partículas de los materiales
elásticos, con la propiedades de resistir y disminuir la energía cinética de
los cuerpos en un periodo de tiempo. Las magnitudes del amortiguamiento que
tiene un sistema estructural, están clasificadas.
- Sistema sobreamortiguado.
- Sistema críticamente amortiguado.
- Sistema subamortiguado.
El amortiguamiento conocido con la letra C en un sistema
real, el factor de amortiguamiento se representa ξ la facción de ese
amortiguamiento en relación al amortiguamiento crítico.
Sistema sobreamortiguado.
Es cuando las vibraciones libres están hipercríticamente
impedidas y si se producen una acción dinámica en la estructura la amplitud de
la vibración disminuye rápidamente.
La edificación retoma su posición de equilibrio sin
vibra, es decir, el movimiento no es oscilatorio por eso es necesario tomarlo
en consideración en el análisis debido a que la masa regresa lentamente a su
posición de equilibrio, estos movimiento se conocen por aperiódicos y en la
práctica se usa en retardadores de movimiento.
Sistema críticamente amortiguado.
Los movimientos no son oscilatorios sino que le sistema
regresa en el menor tiempo posible a su estado de equilibrio estático. El
amortiguamiento crítico es el menor valor de C que resulta de una respuesta sin
vibración. En estos casos no es evidente que los sistemas estructurales en la
práctica se le toma común valor de referencia para determinar el factor de
amortiguamiento necesario para el diseño.
Sistemas subamortiguados.
Este caso es el más visto en las edificaciones y la
amplitud de sus vibraciones decrecen d forma exponencial en un tiempo.
Comúnmente en las edificaciones ξ elvalor del
amortiguamiento varia entre 0.02 y 0.2 en un sistema.
la solución
para el caso homogéneo de la ecuación anterior cuando la excitación de la
derecha de la igualdad es 0 porque la vibración es libre.
Siendo Wd
la frecuencia circular amortiguada, las constantes a y B depende de las
condiciones iniciales en las cuales el sistema se pone en movimiento.
Siendo e la base d los logaritmo naturales e=2.718 es similar al
caso no amortiguado.
El factor de amortiguamiento se obtiene en este caso.
Donde δ el decrecimiento logarítmico de la vibración
debido al amortiguamiento.
Para hallar de forma más directa el valor de
amortiguamiento de una edificación de un grado de libertar, es ponerlo a
vibración libre medir la amplitud del movimiento en dos ciclos
sucesivos. La mayoría de las estructuras, el amortiguamiento es suficientemente
pequeño para que la frecuencia circular.
En un sistema bajo vibración libre con amortiguamiento
está sujeto a un impulso breve, las condiciones iniciales se puede suponer
idénticas al caso de las vibraciones libres no amortiguadas.
La
solución de la vibración libre amortiguada con estas condiciones iniciales.
SISTEMAS CON MÚLTIPLES GRADOS DE LIBERTAD.
Los criterios vistos previamente permiten evaluar la
respuesta de un sistema con un grado de libertad, para cualquier tipo de
impulso aplicado o excitación sísmica. Este caso de una masa concentrada que
tiene la posibilidad de desplazamiento según una dirección. La masa de un
edificio de varios pisos, se distribuye
en función de su altura y puede ser capaz de desplazarse en forma independiente
en sus respectivos niveles.
El movimiento dinámico de este tipo de estructura puede
ser en la práctica mediante coordenadas de desplazamiento independientes. Las
ecuaciones de movimiento de las estructuras múltiples se refieren a un sistema
con masas concentrada a nivel de los pisos, se sobre entiende que los
desplazamientos pueden expresarse mediante un análisis de formas ya
establecidas.
En la figura el pórticos de tres pisos se supone que la
masa de la estructura concentradas a nivel de los dinteles y con posibilidad
únicamente de desplazarse según las direcciones horizontales.
Según este criterio el análisis de los pórticos bajo un movimiento
sísmico se determinan los máximos desplazamiento ua, ub y uc de los diferentes
niveles. La ecuación de desplazamiento en cualquiera de los pisos resulta en consecuencia
la ecuación de equilibrio dinámico de todas las fuerzas actuando sobre la masa
de ese nivel incluyendo las fuerzas exteriores aplicadas, las fuerzas
inerciales y el amortiguamiento.
Se utiliza expresiones similares a las usadas en los
sistemas de un solo grado de libertad la ecuación de equilibrio para un pórtico
de tres pisos se describe.
En los sistemas de masa concentradas en los diferentes
niveles, las fuerzas de inercia se obtiene directamente del producto de cada
masa por su aceleración.
Donde Mn es la masa en el nivel n, y ün la aceleración de
ese nivel, el sistema de ecuaciones se puede escribir en forma matricial.
El método matricial se aplica para cualquier número de
grados de libertad F1 = M ü, donde F1 es el vector de las fuerzas inerciales, M
la matriz diagonal de las masa, y ü el vector de la aceleración.
Es ventajoso crear un matriz diagonal de masas discretas
a nivel de los dinteles, las fuerzas correspondientes a cualquier grado de
libertad van a depender únicamente de la aceleración. Este análisis se vuéleme
complejo cuando la matriz de las masas de un sistema de múltiples grados de
libertad no es diagonal, debido se tiene que introducir nuevas relaciones entre las coordenadas de los desplazamientos.
Las fuerzas elásticas en una estructura dependen del
valor de los desplazamientos y son expresados convenientemente por medio de los coeficientes de influencia de rigideces.
El coeficiente de influencia Kij está definido como la
fuerza correspondiente a la coordenada del desplazamiento i que resulta del
desplazamiento de la coordenada j. En forma matricial se expresa en las
ecuaciones.
Simbólicamente.
FS= K*u
FS es el vector de las fuerzas elásticas, u el vector de
los desplazamiento y K la matriz de la rigidez.
Como se puede presenciar K no es un matriz diagonal por
lo cual su resolución de este sistema no es directa, estas resolución aplica
los conocimientos de las matrices, que en estructuras complejas se resuelve
usualmente con programas de modelados estructurales.
Las fuerzas de amortiguamiento de la primera matriz se
expresan como el producto de un grupo de coeficientes de influencia de
amortiguamiento por las velocidades en los desplazamientos según los grados de
libertad. El amortiguamiento puede escribirse en forma análoga a las fuerzas
elásticas FD= Cύ, en donde Fd es el vector de las fuerzas de amortiguamiento, ύ
es el vector de la velocidad y ce la matriz de amortiguamiento.
RESPUESTA ESTRUCTURAL A SISMOS.
El problema principal estructural en el caso de un
movimiento sísmico, es determinar los desplazamientos producidos, los cuales se
derivan las fuerzas internas y el estado tensional de una estructura. La masa
de un sísmate se determina en función de las cargas permanentes más un
porcentaje de las cargas variables, aplicando apropiadas factores de
resistencia de reducción y se debe suponer que no todos los niveles estarán
soportando la carga variable máxima.
Las estructuras tiene rigidez la cual se obtiene de la
relación de carga-desplazamiento aplicado de los principios de resistencia de
los materiales y de su elasticidad, y tomando en cuenta factores como la
flexibilidad de las uniones o juntas en las estructuras de acero y la presencia
de las fisuras en los elementos del concreto armado.
Las estructuras es posible plantear con rapidez las
matrices representativas a la masa y la rigidez de los sistemas, pero no es de forma tan directa obtener la
matriz de amortiguamiento, porque esta depende de la forma como se produce la
disipación de energía en una edificación. Es usual estimar el amortiguamiento
con un valor similar definido por las estructuras existentes, obtenidos por
experiencias previas.
Los movimientos sísmicos son frecuencias en el mundo, y
cada caso es posible lograr registro por medio de los acelero gramas. Estos
aparatos permiten conocer las variaciones de la aceleración del suelo en
función del tiempo, según tres componentes ortogonales de la aceleración, con
las cuales se puede integrara para obtener las velocidades y los
correspondientes desplazamientos.
En un edificio es posible calcular los movimientos
horizontales, la velocidad, la aceleración, el corte basal, las respectivas
fuerzas inerciales y las solicitaciones, en base a los datos que resultan de un
acelero grama, se puede aplicar criterios dinámicos y estáticos.
Un análisis dinámico se le realiza a una estructura de
gran altura, requiere un gran trabajo, especialmente si se produce zonas de
plastificación localizada que varias la frecuencia propia natural del sistema a
medida que progresa la metástasis. En la mayoría e los casos llevar a cabo un
análisis estático con fuerzas inerciales se supone que le sistema vibra en su
modo fundamental, para tomar en consideración los modos superiores de
vibración, se debe aplicar un fuerza concentrada horizontal en el tope de la
edificación.
Las cargas laterales restantes distribuidas en la altura
de la estructura son proporcionales al producto de la masa en cada nivel por su
altura con respecto a la base, dando por resultado una carga triangular
invertida con el vértice de apoyo.
El análisis estático equivalente se obtiene una respuesta
similar al método dinámico, en general este análisis estático permite lograr
resultados suficientes aproximados para predisieño dela estructura y facilita
la determinación con mayor precisión del valor de masas del sistema.
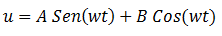
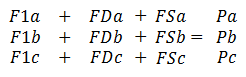
No hay comentarios:
Publicar un comentario